METODE BAGI DUA
Misalkan kita telah menemukan
selang [a,b] sehingga f(a)f(b)<0. Pada setiap kali lelaran, selang [a,b]
kita bagi dua di x = c , sehingga terdapat dua buah selang yang berukuran sama,
yaitu selang [a,c] dan [c,b] selang yang kan diambil berikutnya tergantung
apakah f(a)f(c) < 0 ataau f(c)f(b) <0. Selan yang baru itu dibagi dua
dibagi dengan cara yang sama. Begitu seterusnya sampai ukuran selang yang baru
sudah sangat kecil.
Teorema 1.1 jika f(x) menerus
didalam selang [a,b] dengan f(a)f(b) < 0 dan s € [a,b] sehingga f(x) = 0 dan
cr = (ar + br )/2, maka selalu berlaku dua
ketidaksamaan berikut :
Misalnya didapat sebuah
selang dengan batas [a,b] dengan f(x) adalah fungsi yang akan dicari akarnya
dengan (epsilon)
adalah batas maximum galat yang ditentukan dan c adalah selang baru dengan
galat mendekati epsilon maka :
(epsilon)
adalah batas maximum galat yang ditentukan dan c adalah selang baru dengan
galat mendekati epsilon maka :
(p.1)
Dengan f(a),f(b),f(c) adalah
f(x) untuk masing-masing batasan yang ditentukan,jika
f(a) * f(c) < 0
(p.2)
maka b = c sehingga selang
berikutnya untuk [a,b] = [a,c] sebaliknya , jika
f(a)*f(c) > 0
maka a = c sehingga selang
berikutnya untuk [a,b] = [c,b]
dengan
(p.3)
Demikian cara ini diulang
sehingga memenuhi L < epsilon , dan jumlah lelaran yang diperlukan dapat
dihitung dengan :
download
- sintaks mathlab
- contoh soal serta jawabanya di
jika tidak bisa mendownload silakan baca
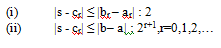





Tidak ada komentar:
Posting Komentar